在這篇遊戲《群星》的經濟指南里，我將建立對遊戲中各類資源價格進行量化計算的理論框架；然後，我會提供一個現成的Excel表格，供玩家自己在遊戲里完成該量化計算；最後，我將介紹如何利用價格信息實現利益的最大化。
第一章：勞動價值論
勞動價值論指出：價值是凝結在商品中的無差別的人類勞動；商品的價值量由生產商品的社會必要勞動時間決定。
這段話也經常用以下的數學公式來表達：
C + L = WC：Capital，商品生產期間材料、耗材、工具、廠房和土地租賃等資本的價值。
L：Labor，商品生產期間所消耗的人類勞動的價值。
W：Worth，所生產出來商品的價值。（W其實是德語Wert的縮寫，也是Worth的意思。導師是德國人）
用人話來講就是：
輸入商品的價值 + 勞動產生的增值 = 輸出商品的價值第一章：量化計算在《群星》里，一個發電廠的技工每月生活開支消費1食物和0.25消費品，勞動所得為6能量。套用勞動價值論的公式，我們可以得到下面的等式：
1F + 0.25C + 1P = 6E.F：Food，食物；
C：Consumer Goods，消費品；
P：PoP，1個人口一個月的勞動價值
E：Energy，能量
導師教導我們，價值是凝結在商品中的無差別的人類勞動。無論是誰，在相同的勞動效率下，任何一個人相同勞動時間產出的勞動價值是一樣的。也就是說，統治者一個月的勞動價值和一個奴隸一個月的勞動價值是一樣的。拋開現實世界不談，在《群星》這款遊戲里，這個理論是完全站得住腳的。從開上帝視角的玩家來看，每個人口都是一樣的，我根本不關心這個人口具體是統治者還是奴隸，對我來說他們都是完全一樣的生產資源。人口屬於不同社會階級的現象，只是遊戲里工作崗位數量的結構分布導致的必然結果。簡單來講，總要有人去挖礦，也總要有人在辦公室從事研究，這是社會分工的需要，而不是工作本身有貴賤之分。在《群星》的遊戲里，當社會提供的工作崗位在結構和數量上發生變化時，今天的統治者，可能過幾個月就要去當勞工，反之亦然。
所以，當我們將馬克思勞動價值論的公式拓展到遊戲中的其他資源生產崗位時，這些崗位的每月勞動價值都是一樣的，也即都是同一個數值P。請記住，P代表1個人口一個月的勞動價值。
在群星里，各資源生產崗位的初始工作輸入和輸出狀態如下：
發電廠技工：每月生活開支消費1食物（F）和0.25消費品（C），產出6能量（E）；採礦區礦工：每月生活開支消費1食物（F）和0.25消費品（C），產出4礦物（M）；農業區農民：每月生活開支消費1食物（F）和0.25消費品（C），產出6食物（F）；專家崗工匠：每月生活開支消費1食物（F）和0.5消費品（C），消耗原材料6礦物（M），產出6消費品（C）專家崗冶金：每月生活開支消費1食物（F）和0.5消費品（C），消耗原材料6礦物（M），產出3合金（A）資源生產崗：每月生活開支消費1食物（F）和0.5消費品（C），消耗原材料10礦物（M），產出2資源（S）備註：由於工匠、冶金和資源崗為專家人口，所以其日常消費品消耗比勞工人口（技工、礦工、農民）高0.25。
應用勞動價值理論，我們可以將上述工作崗位的資源生產過程用數學表達式來記錄，於是我們得到一組很重要的等式（線性方程組）。
技工: 1F + 0.25C + 1P = 6E礦工: 1F + 0.25C + 1P= 4M農民: 1F + 0.25C + 1P = 6F工匠: 6M + 1F + 0.5C + 1P = 6C冶金: 6M + 1F + 0.5C + 1P = 3A資源生產崗位: 10M + 1F + 0.5C + 1P = 2SF：Food，食物；
C：Consumer Goods，消費品；
E：Energy，能量；
P：PoP，1個人口一個月的勞動價值；
M：Mineral，礦物；
A：Alloy，合金；
S：Strategic Resource，戰略資源（氣體、微粒、水晶）
群星里的主要經濟資源初中的時候，我們都學習過如何求解像下圖一樣的一個線性方程組。
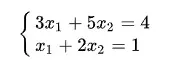
我們使用勞動價值論後，從《群星》各個資源生產崗位得到的也是一個線性方程組，要求的解（未知數）就是E、M、F、C、A、S、P。作為一名中國人的基本數學修養要求我們看到方程組的第一反應就是求這個方程組的解。簡單的求解過程我們直接略過，反正後面也是用電腦來做計算，下面我直接給出解：
1 M = 1.5 E1 F = 1.0 E1 C = 2.6 E1 A = 5.2 E1 S = 10.8 E1 P = 4.3 E在《群星》遊戲里，能量（Energy）是作為基礎貨幣存在的，可以用於直接購買各類資源。所以，上述解是以能量為單位給出的。
1F=1E表達的意思是：1單位食物值1單位能量。上述解與遊戲里默認的市場價格十分接近。
第一章：量化結果的內涵在這一章，我們通過對馬克思勞動價值論公式的應用和推廣，得到了一個線性方程組。通過解線性方程組，我們量化計算出了各個資源的價格。
1個食物價值1個能量，是因為食物和能量的生產效率是一樣的。1個人口在消耗1食物和0.25消費品的情況下，每月能生產6食物或6能量。1個礦價值1.5個能量，是因為與生產能量相比，生產相同數量的礦，需要消耗更多的人口勞動時間。1個人口在消耗1食物和0.25消費品的情況下，每月分別能生產4礦和6能量。以《群星》遊戲里相對簡單的人口和經濟機製作為例子，大家再重溫一遍經典，一定能更好的理解導師在《資本論》里要表達的意思。
價值是一般人類勞動的凝結，它構成商品交換的基礎。商品價值量的大小由生產商品時所耗費的一般人類勞動量決定，計量勞動量多少的自然尺度是勞動時間，即價值量決定於勞動時間。商品交換以價值量為基礎，遵守等量社會必要勞動相交換的原則。
交換價值以防各位第四天災們沒能理解導師的經典著作，我就再啰唆幾句吧。
上面給出的解是以能量（E）為計價單位的，這種表現形式的優點是便於在遊戲里直接使用，畢竟遊戲里各種資源在市場上是以能量（E）標價的。但是，我們其實也可以將上面的解等效改寫成以人口每月勞動的價值（P）為計價單位的形式。
1 M = 0.35 P1 F = 0.23 P1 C = 0.60 P1 A = 1.21 P1 S = 2.51 P1 E = 0.23 P兩種形式的解是彼此等價的。等式「1 P = 4.3 E」 反過來就是 「1 E = 0.23 P」。而以P計價的解，其實就是「商品價值是凝結在商品中的無差別人類勞動」的數學表現形式。
價值是一個商品經濟范疇。產品成為商品以交換為前提。交換就有個比率的問題。價值以這個比率，也就是以交換價值為其具體的表達形式，解的本質是給出了各類資源的合理交換比率，所以，解用哪種資源作為計價單位是無所謂的。更換解的計價單位，並不會改變各類資源的交換比率，比如，M/E的比率會一直是1.5，F/E的比率也會一直是1.0。只是在各種形式的計價單位裡面能量（E）和人口每月勞動價值（P）是最具有現實意義的。
一般等價物使用能量（E）計價是因為方便，畢竟市場里各種資源是以能量（E）來標價的。但是，我們知道能量（E）只是一般等價物，一般等價物作為商品交換的媒介，起著貨幣的作用，但它不是貨幣。同時，即使貨幣也存在貨幣超發貶值和通縮升值的問題，導致我們很難用貨幣對資源的價值量進行計量。比如，當資源價格上升的時候，你無法確定究竟是資源本身的價值上升了，還是因為貨幣超發了。
一般等價物本身就是一種商品。同所有其他商品一樣，它本身的交換價值也是由生產它的社會必需勞動量所決定的。此後，所有其他商品便在同這個真實的交換價值比較下，表現出本身的交換價值。作為商品，一般等價物也保存著一定的使用價值。這一使用價值是由它的天然屬性決定的。
勞動時間而使用人口每月勞動價值（P）計價，就不存在這個問題。因為我們沒有使用一般等價物，而是直接使用了資源的價值（勞動時間），對其進行計價。畢竟，衡量資源交換比率的基礎，其實就是勞動時間。以（P）計價，我們能直觀的看出社會生產各類資源的生產效率。各類資源價值（勞動時間）的變化，直接體現的是其生產效率隨科技和社會發展的變化。這種形式的解，所得到的數值結果不會受到通貨膨脹或收縮的影響。
1 M = 0.35 P
1 F = 0.23 P
1 C = 0.60 P
1 A = 1.21 P
1 S = 2.51 P
1 E = 0.23 P
第二章：絕對優勢1776年，亞當·斯密出版《國富論》這部經典著作。在書中，亞當·斯密認為自由貿易才是國家之間經濟交易的最優政策，通過自由貿易，每個國家都能專業化生產那些本國具有絕對優勢（比其他國家生產效率更高）的產品，同時進口那些本國具有絕對劣勢（比其他國家生產效率更低）的產品。他主張，如果外國的產品比自己國內生產的要便宜，那麼最好是輸出在本國有利的生產條件下生產的產品，去交換外國的產品，而不要自己去生產。第一章我們建立量化計算的理論框架時，用的是遊戲里資源生產的簡化例子，我們未考慮法令、政策、科技、人口特性、思潮、政體等等的修正。這些修正都會被第三章的量化計算器所涵蓋。
在實際的遊戲里，由於上述修正的存在，每個帝國的各類資源生產效率是不一樣的。要實現星際合作的雙贏目標，我們要優先發展出自己的優勢資源，然後集中力量生產優勢資源，以去交易其他資源。如此，我們就能通過交易，實現帝國生產效率的提升。
基礎資源在三種基礎資源（能量、礦物、食物）里，能量是最適合作為優勢資源的。
首先，能量是遊戲里的一般等價物。市場里所有的資源均以能量計價，行商艦隊、貿易商、策展人、藝術家 、虛境行者、打撈者、傭兵都用能量幣進行交易。
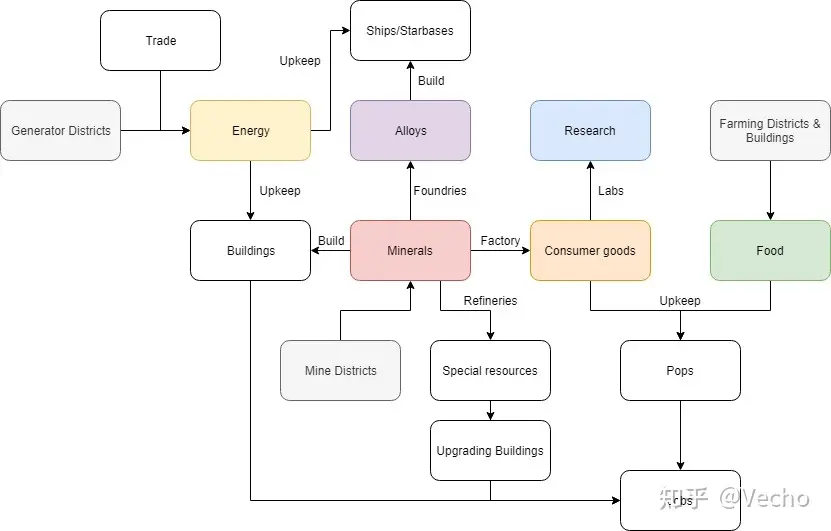
其次，能量在遊戲里具有最廣泛的用途。能量幣可以用來支付建築、艦船、空間站、恆星基地、法令等的維護費，也可以用於清除障礙和改造星球。在3.5版後，星球的自動管理也能使用能量替代礦物來完成星球上的建設工作，所以你現在也可以用能量來支付建築費用了。這就導致，礦物的主要用途只剩下了生產消費品和合金。
最後，在相同科技水平下，能量的生產效率一直高於礦物。第一章的例子里，我們就知道了開局時1 M = 1.5 E。
基於上述分析，我遊戲時的經濟策略一直是：不用自己的人口挖礦，而通過交易補礦。沒必要把自己的寶貴人口浪費在一個低效的生產崗位上。我礦的來源主要是，星系的自然產出+每月市場購入50礦+AI交易。當我對經濟結構進行這樣的傾斜後，遊戲的前中期，我也不爬挖礦的科技了，而是把省下來的科技點數優先投入提高能源生產的科技。我也沒必要騰出一個星球專門用於挖礦。我一般是在遊戲後期，物質分解器都造出來了，礦還不夠用，然後我又和全世界為敵的情況下，才自己挖礦。買的比自己造的還便宜，那幹嘛不直接買呢。
經濟政策我們知道，在《群星》里「經濟政策」有「民用經濟」、「混合經濟」和「軍事經濟」三種傾向。消費品只有滿足人口消費需求一種用途，而合金則要用於建造恆星基地、艦船和巨構等更重要的地方。合金多多益善，永遠不嫌多；消費品則是夠用即可，多了並無價值。所以，我會一直選擇「軍事經濟」，享受+25%的合金生產效率，然後盡量從市場和AI處購得消費品，來迴避-25%的消費品生產效率。
經濟政策的三種選擇第二章：金融煉金術
那些想通過投機獲得成功的人應該學會一個簡單的道理：在你買入或是賣出之前，你必須仔細研究，確認是否是你進場的最好時機。只有這樣，你才能保證你的頭寸是正確的頭寸。——《股票大作手回憶錄》從金融的視角來看，我們可以把遊戲里的經濟收益分成3類：
第一類，通過投入勞動力而獲得產出的生產活動，類似現實世界的實體經濟；
第二類，通過初期一次性投入，獲得未來的一筆持續現金流的投資活動。占據一個新的星系、建設一個蓋滿太陽能面板的恆星基地和建設巨構，都屬於投資活動。此類活動獲得的是未來持續的收益，且不需要投入勞動力；
第三類，則是金融煉金術，我們不從事生產，也不做投資，我們將我們手中的所有經濟資源（食物、礦物、能量、消費品、合金、戰略資源）作為交易的資本，通過不斷的與市場和AI進行交易，持續的做高拋低吸的操作。我們不創造價值，但通過我們的資本運作，我們最後將AI的資源掠奪到我們自己的手裡。
亞當·斯密所提倡的互惠互利、專業化分工的國際貿易已經是昨日黃花。掌握勞動價值理論的我們，能精確的計算商品的真實價值，我們要充分利用這一信息不對稱的優勢，主動的與市場和AI進行套利交易。
當星際市場開放後，我經常在上面大量買進（礦物、消費品）或賣出（合金）。由於我知道商品的真實價值，我進行的每一筆交易都是對我有利的。通過此類交易獲取的收益是無成本的，我完全是空手套白狼，點石為金。
AI在交易時有個特點，就是對戰略資源（氣體、微粒、水晶）的估值給的特別高。如下圖所示，AI願意用4110能量和我交易100微粒，相當於是用41.1能量的價格來買我的微粒。
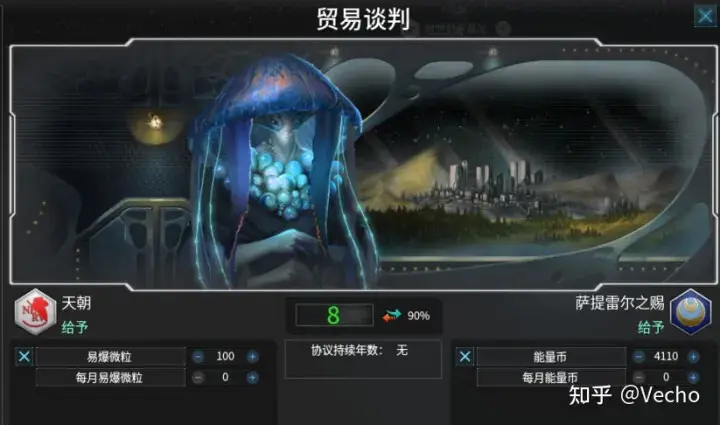
利用這一點，我經常會大量的用戰略資源交易AI的基礎資源（礦物、能量、食物），然後AI會去星際市場上賣出手頭多餘的戰略資源，這會導致星際市場上戰略資源價格出現下跌，於是我又從星際市場上大量購入價格下跌的戰略資源。左手賣出，右手買進，掙著兩倍的利潤，還可以循環往復不斷操作。
更歹毒的是，我會刻意大量收購AI的基礎資源，我不僅會盡量榨乾AI的資源庫存，我還會與AI簽訂30年的購入合同，將AI基礎資源的月收入也盡量的拉低。一套操作下來，AI的經濟基本就崩潰了，因為AI沒有足夠的基礎資源用於發展經濟，AI經濟陷入了停滯的狀態。而我通過金融戰爭，達到不戰而屈人之兵的效果。
第三章：計算器第一章進行理論推導時，我用的是個簡化的例子，而這一章我們要將遊戲里的各種加成（modifier）考慮進去，精確計算遊戲里各類資源的真實價格。
懶惰是人類進步的第一原動力，我用Excel做了個計算器。很簡單，長這個樣子。
你需要做的是：
根據遊戲里的實際數據填寫綠色區域A3:G8和H3:M8的單元格。綠色區域A3:G8的單元格數據來源於遊戲里崗位提示窗口；綠色區域H3:M8單元格數據來源遊戲里的區劃和建築，這個區域也可以不填。
拷貝橙色區域P3:W8單元格的數據，黏貼到Octave網站里，回車。
拷貝橙色區域Y3:AA9單元格的數據，黏貼到Octave網站里，回車。
將Octave網站里的計算結果，拷貝到紅色區域AD3:AD8的單元格。
計算器下載地址：
鏈接：https://pan.baidu.com/s/1ZPhex4WETHIOdFA5pW8-zw?pwd=vobq 提取碼：vobq我將以我2355年的一個檔作為例子，來講解如何使用這個Excel來進行量化計算。
第三章：解線性方程組在講解具體如何操作前，有必要交代一下整個計算過程的思路。
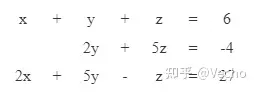
在大學的線性代數課上，我們都學過，上述的方程組可以用矩陣格式來表達。
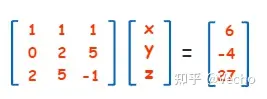
更簡單的，我們可以用向量來表達這個方程組：
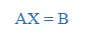
如果要求解x，我們只需要按下圖來計算即可。這是個干凈利落和優雅的解法，並且：人來想，電腦來做。
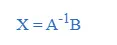
所以，在Octave（在線的矩陣計算器）里，我們只需要輸入：
A = [.....]B = [.....]x = A\B然後就能得到方程組的解了。
所以，Excel表格里的綠色區域負責收集遊戲里的原始數據，橙色區域則有兩個目的：
將兩個綠色區域的數據進行匯總疊加；
將數據以Octave能識別的格式進行記錄；
第三章：填寫綠色區域A3:G8和H3:M8單元格的數據以技工為例，遊戲里的提示窗口顯示，技工生產24.5能量（E），消耗1.1食物（F）和0.2消費品（C）。所以，我在單元格B3里填入24.5，在單元格C3填入-1.1，在單元格E3填入-0.2。填的時候注意，生產出來的用＋號，消耗的用－號。
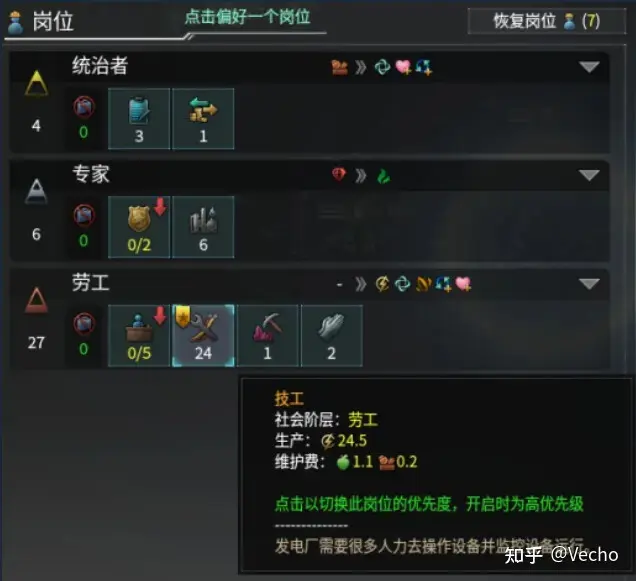
備註：人口的食物維護費是1.1，是因為我開了個人口食物消耗增加10%的法令。人口的消費品消耗是0.2，是因為我點了個人口、區劃、建築維護費減10%的傳統。
技工需要發電區劃提供崗位，還需要建築（能源中樞）提高產能。一個發電區劃的維護費是0.9E，提供2崗位。建築（能源中樞）的維護費是1.8E和0.9S，建築維護費由24個技工共同承擔。所以，我在單元格H3里填入「=-0.9/2-1.8/24」，在單元格M3里填入「=-0.9/24」。
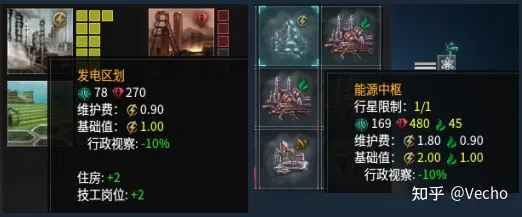
其他崗位也是一樣的操作方法。
備註：
工匠B6單元格里有+2（E），是因為我有能工巧匠的特長，工匠會提供額外的+2貿易，這+2貿易最後變成了+2能量。
綠色區域A3:G8單元格的數據內容是「生產 - 消耗」。以農民為例，食物維護費是1.1，食物產出是30.1，所以在D5單元格里我填寫的是「=-1.1+30.1」（F）。
第三章：把橙色區域的數據拷貝到OctaveOctave是一個線上進行矩陣運算的網站。
https://octave-online.net/
第一步，將橙色區域P3:W8單元格的數據黏貼到Octave網站里，回車。
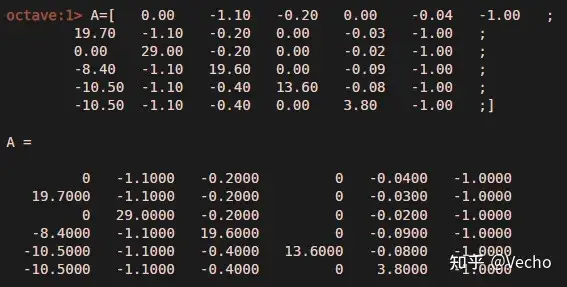這一步是告訴Octave，A = [.....]第二步，將橙色區域Y3:AA9單元格的數據，黏貼到Octave網站里，回車。
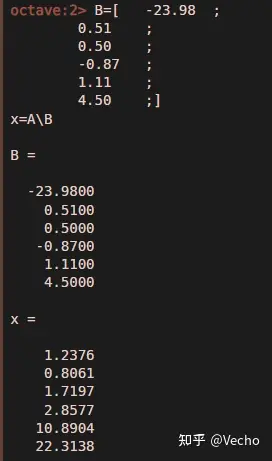這一步是告訴Octave，B = [.....]，然後x = A\B，求解x。第三章：將Octave網站里的計算結果拷貝出來如下圖，把Octave網站里「x =」以下的計算結果，拷貝到紅色區域AD3:AD8的單元格。
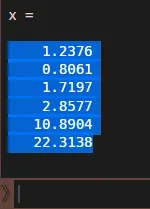第三章：小結經過以上的操作，我們就得到遊戲里各類資源以能量計價的價格了。礦物價格為1.2能量，是因為即使到遊戲後期，礦物的生產效率還是低於能量。食物價格為0.8能量，是因為我產食物的星球有+40%食物產出的Buff，導致我食物的生產效率比能量還高。
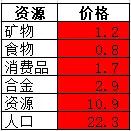
如果你比較懶的話，綠色區域H3:M8的數據也可以不填，因為對計算結果影響很小。畢竟建築的維護費被多個人口一攤，也就沒多少了。區劃的維護費，本來就不高，礦物、食物和能量區劃的維護費是0.5E每人口，消費品、合金區劃的維護費也只是1E每人口。
後記本來是隨筆的，寫著寫著就7000多字了，眼看又變成收藏比贊多。小眾優質作品創作不易，大家覺得好的話就收藏的時候順帶點個贊吧，讓更多的人能看到。謝謝。
